Nachdem der Sobel-Operator den Farbverlauf des Bildes bereitgestellt hat, sind wir fast schon dabei, die Ränder des Dokuments zu finden. Wenn Sie nicht wissen, was der Sobel-Operator ist, empfehle ich dringend, zuerst den vorherigen Artikel der Serie zu lesen.
Es ist jedoch nicht sinnvoll, eine visuelle Darstellung der Kanten zu haben. Wir brauchen mathematische Darstellungen für jede Kante im Bild, um ihre Schnittpunkte (die Ecken des Dokuments) zu finden, wofür wir die Hough-Transformation verwenden können.
Die Hough-Transformation ermöglicht es uns, unter Verwendung eines Bucket-Voting-Systems unvollkommene Übereinstimmungen für beliebige visuelle Muster zu finden. Es gibt zwei Möglichkeiten, diesen Algorithmus zu verstehen:mathematisch und intuitiv. Lassen Sie uns beide durchgehen, bevor wir diskutieren, wie wir es implementieren können.
Mathematisch ausgedrückt
Da die Hough-Transformation technisch gesehen Kreise, Ellipsen, Dreiecke oder andere beliebige Muster finden kann, benötigen wir eine individuelle mathematische Analyse für jeden Mustertyp, den wir erkennen möchten.
Für die Zwecke dieses Projekts haben wir nach Linien gesucht, für die die Hough-Transformation ursprünglich entwickelt wurde und die daher am einfachsten zu erkennen sind. (Wenn Sie sich fragen, warum wir nicht einfach nach Rechtecken suchen, um das Dokument zu finden, kommen wir am Ende dazu).
Lassen Sie uns zunächst entscheiden, wie wir unsere Linien mathematisch darstellen wollen. Eine natürliche Wahl könnte das berühmte sein:
y=mx+b
Dieses Formular ermöglicht es uns, jede Linie darzustellen, die möglicherweise im 2-D-Raum existieren könnte, indem die Parameter m (die Steigung der Linie) und b (der y-Achsenabschnitt) modifiziert werden. Wenn wir eine Linie mit einer 30-Grad-Neigung wollen, die 1200 Pixel vom unteren Rand des Bildes entfernt ist, können wir Folgendes verwenden:
m=tan30°b=1200spacey=0,577x+1200Dies erscheint auch visuell korrekt, wenn es gezeichnet wird:
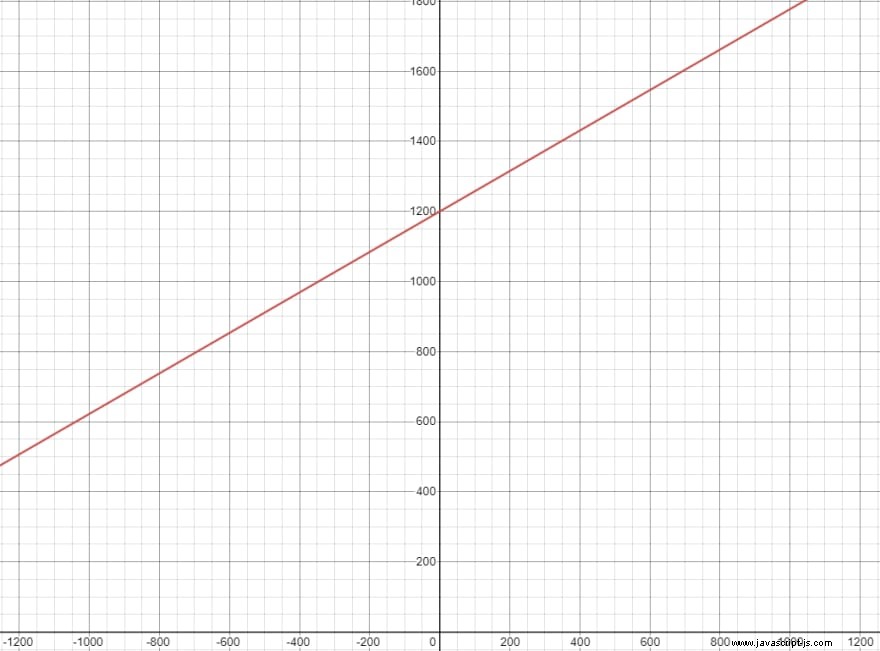
Das einzige Problem bei dieser Darstellung ist, was passiert, wenn wir versuchen, eine vertikale Linie zu erstellen. Vertikale Linien bewegen sich nicht horizontal, ihr Verlauf ist immer Null, während ihr Anstieg eine beliebige Zahl ist. Technisch gesehen können wir entweder positive oder negative Unendlichkeit verwenden, um die Steigung darzustellen, aber dann hätten wir keine Möglichkeit zu wissen, wo sich die Gerade auf der x-Achse befindet, da diese Gleichung nur den y-Achsenabschnitt angibt.
Obwohl es möglich ist, dieses Problem zu umgehen, ist es auch wichtig, die Tatsache zu berücksichtigen, dass wir in der Lage sein möchten, zwischen visuell unterschiedlichen Linien zu unterscheiden, aber diese Form erschwert dies. Betrachten Sie diese vier Zeilen:
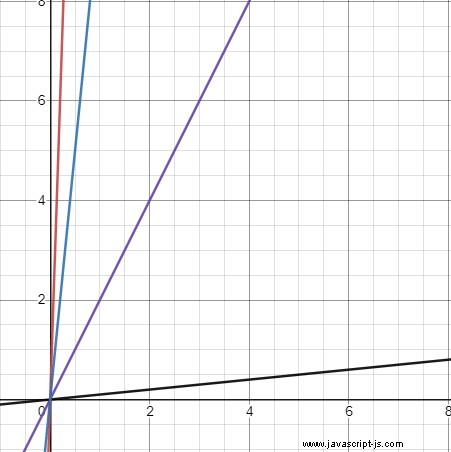
Die schwarze Linie hat eine Steigung von 0,1 (d. h. m =0,1), die violette Linie eine Steigung von 2, die blaue Linie eine Steigung von 10 und die rote Linie eine Steigung von 30.
Obwohl die roten und blauen Linien visuell sehr ähnlich sind, variieren ihre Steigungen um 20, und obwohl die violetten und schwarzen Linien unterschiedlich erscheinen, unterscheiden sich ihre Steigungen nur um 1,9. Wenn wir Steigung verwenden wollen, müssten wir einen Weg finden, kleine Unterschiede in der Steigung bei niedrigeren Werten hervorzuheben.
Anstatt sich mit all diesen Problemen zu befassen, können wir die Linien mithilfe von Polarkoordinaten genauer darstellen.
"Normale" Koordinaten werden auch als kartesische Koordinaten bezeichnet:Sie werden als (x, y) dargestellt , wobei x die Position auf der horizontalen Achse und y die Position auf der vertikalen Achse ist. Polarkoordinaten werden stattdessen als (r, Θ) dargestellt , wobei r der Abstand vom Ursprung und Theta der Winkel gegen den Uhrzeigersinn von der positiven x-Achse in kartesischen Koordinaten ist. Hier sind einige Beispiele:
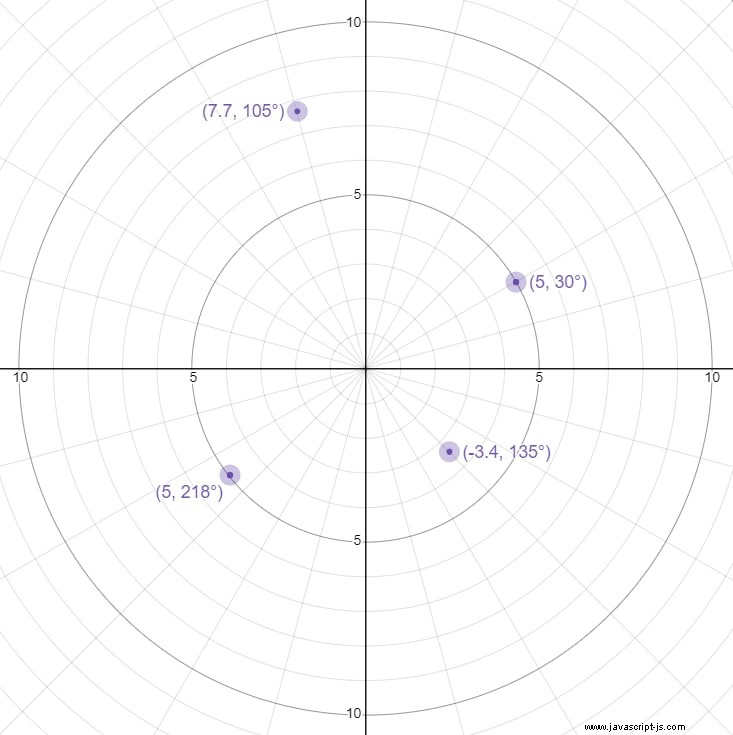
Polarkoordinaten und kartesische Koordinaten erfüllen immer die folgenden Gleichungen:
x=rcosθy=rsinθspacer=x2+y2θ=atan2(y,x)
Obwohl wir unsere ursprüngliche Form y = mx + b umwandeln können in polar, würden wir am Ende mit den gleichen Problemen in Bezug auf visuelle Ähnlichkeit und vertikale Linien enden. Stattdessen können wir die Hesse-Normalform verwenden, die Linien mit einer einzigen Polarkoordinate darstellen kann.
Die meisten Online-Erklärungen machen die Hesse-Normalform komplizierter als für unsere Zwecke erforderlich, daher hier eine intuitive Erklärung. Stellen Sie sich vor, Sie haben eine beliebige Polarkoordinate. Zeichnen Sie ein Segment vom Ursprung zu dieser Koordinate. Zeichnen Sie nun eine Linie senkrecht zu dem Segment, das die Koordinate enthält. Diese Linie wird durch die Polarkoordinate eindeutig identifiziert.
Hier ist eine Grafik, wie das aussieht:
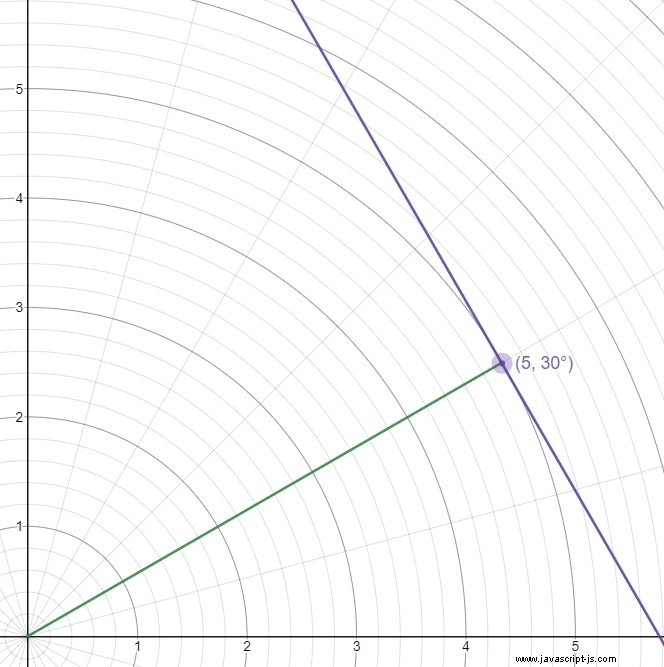
Das grüne Liniensegment verbindet den Ursprung mit dem Punkt, also ist die senkrechte lila Linie die Linie, die wir mit dem Punkt (5, 30°) beschreiben können .
Dies gibt uns eine einfache Möglichkeit, zwischen Linien zu unterscheiden:Wenn die Punkte weit voneinander entfernt sind, sind die Linien visuell unterschiedlich. Es gibt keine Fälle mehr, in denen eine kleine Änderung einer Variablen eine große visuelle Änderung für die Linie verursacht, da r und Theta jeweils einen "linearen" visuellen Effekt haben. Beispielsweise bewirkt eine Theta-Änderung von 10° immer einen ähnlichen visuellen Unterschied für die Linie, unabhängig vom genauen Theta-Wert.
Noch wichtiger ist, dass die Hesse-Normalform es einfach macht, die Linien zu finden, auf denen eine Koordinate im kartesischen Raum liegt. Kennen wir den Winkel Θ in Hesse-Normalform und haben eine kartesische Koordinate (x, y) diese Linie durchläuft, können wir nach r auflösen:
In der obigen Gleichung erzeugen zwei beliebige Punkte, die auf derselben Winkellinie Θ liegen, denselben Wert von r. Wir werden bald diskutieren, warum diese Qualität so wichtig ist. Im Moment werde ich eine intuitive Erklärung des Abstimmungsprozesses in der Hough-Transformation geben.
Farbeimer
Stellen Sie sich vor, Sie hätten die Aufgabe, die häufigste Farbe aus einer Million Eimern zu finden.
Eine Lösung könnte darin bestehen, jeden Eimer durchzugehen und zu zählen, wie viele Eimer Sie mit jeder Farbe gesehen haben. Dieser Ansatz bietet jedoch nur eine sehr begrenzte Genauigkeit:Sie können keine genaue Farbe angeben, sondern etwas Allgemeines wie "Grün" oder "Gelb". Außerdem berücksichtigt diese Lösung keine Schwankungen in der Farbmenge pro Eimer.
Eine bessere Lösung wäre, ein großes Raster aus leeren Farbtanks zu erstellen, wobei das Aufwärtsgehen des Rasters hellere Farben und das Bewegen zu beiden Seiten einen anderen Farbton ergibt. Mit anderen Worten, wir könnten herausfinden, wo in dem folgenden Diagramm jede Farbe liegt:
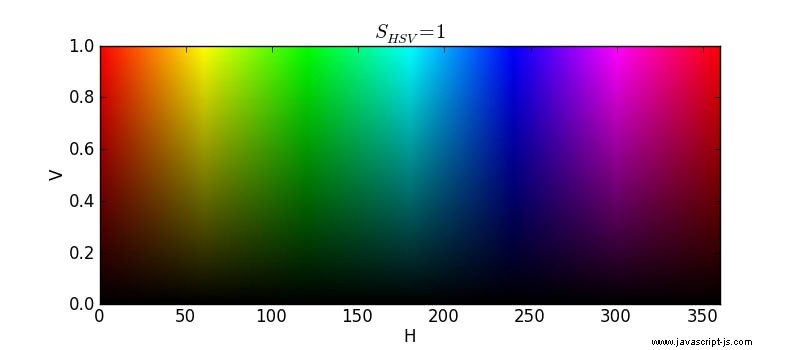
Ich weiß, dass dieses Diagramm die Sättigung nicht berücksichtigt, aber für die Zwecke dieses Beispiels können wir davon ausgehen, dass jede Farbe vollständig gesättigt ist.
Stellen Sie sich vor, dass es Gitterlinien entlang jedem Farbtongrad und jeder 0,01-Werterhöhung im obigen Diagramm gibt. Wir können den Farbton und Wert jedes Farbeimers abschätzen und dann den Inhalt des Eimers in den Tank im Gitter entleeren, der diesem Farbton und Wert entspricht.
Wenn wir zum Beispiel auf einen Eimer mit dunkelroter Farbe stoßen, würden wir ihn in einen der Tanks in der unteren linken Ecke des Gitters kippen (da der untere Bereich dunklere Farben und der linke Bereich rote Farben hat).
Am Ende konnten wir die Tanks mit den meisten Farben finden, um die häufigste Farbe in der Farbe zu bestimmen.
Dieser Ansatz löst zwei der Probleme mit unserem ursprünglichen Zählansatz. Da wir die Eimer in ein Gitter ausgießen, berücksichtigen wir alle Unterschiede in der Farbmenge pro Eimer genau. Noch wichtiger ist, dass unser Endergebnis eine exakte Farbe ist, und theoretisch ist der maximale Fehler gegenüber der wirklich häufigsten Farbe die Fläche eines Tanks (ein Grad Fehler im Farbton und 0,01 Fehler im Wert).
Es ist wichtig zu beachten, dass dieser Ansatz eine schlechte Wahl wäre, wenn wir nicht so viele Farbeimer wie Datenpunkte hätten. Wenn es beispielsweise nur ein paar tausend Eimer gäbe, wäre die Mehrheit der 18.000 Tanks vollständig leer, nachdem wir die gesamte Farbe ausgegossen hätten, und kleine Fehler bei unserer Annäherung an die Farbe würden zu falschen Ergebnissen führen.
Wenn wir beispielsweise zehn Eimer mit fast genau demselben Gelbton und leicht unterschiedlicher Helligkeit finden, könnten wir sie in zehn separate Tanks stellen, während zwei hellrote Farbeimer, von denen wir schätzen, dass sie genau denselben Farbton und dieselbe Helligkeit haben, hineingehen würden der gleiche Panzer. Am Ende würden wir in dem hellroten Tank zwei Eimer Farbe finden und in jedem der gelben Tanks nur einen Eimer, sodass unser Algorithmus entscheiden würde, dass Rot die häufigste Farbe ist, obwohl Gelb eindeutig häufiger vorkommt.
Wohin führt diese Analogie?
Wenn Sie sich an früher erinnern, haben wir besprochen, wie die Hesse-Normalform uns jede Linie mit einem Punkt in Polarkoordinaten darstellen lässt und wie visuell ähnliche Linien durch Koordinaten dargestellt werden können, die mathematisch nahe beieinander liegen. Lassen Sie uns diskutieren, wie wir es tatsächlich verwenden können, um Linien in unserem Verlaufsbild zu finden.
Für jedes Pixel im Bild können wir alle Linien finden, die durch das Bild verlaufen und auf denen das Pixel möglicherweise liegen könnte. Fürs Erste gehen wir davon aus, dass eine Linie in alle Richtungen möglich ist. Wir können eine Schleife von Θ =0° bis Θ =179° in Ein-Grad-Schritten machen und nach r auflösen, indem wir die Gleichung von früher verwenden, um 180 potenzielle Linien in der Hesse-Normalform (r, Θ) zu finden pro Pixel. (Beachten Sie, dass wir nicht auf 359° gehen, da sich Linien unendlich in zwei entgegengesetzte Richtungen erstrecken, sodass jeder Winkel über 180° eine Linie ergibt, die mit einem Winkel unter 180° identisch ist.)
Jetzt haben wir also 180 mathematische Linien pro Pixel im Bild. Was können wir eigentlich damit machen?
Denken Sie daran, dass wir versuchen, die Linien zu finden, die den Kanten im Bild entsprechen. mit anderen Worten, Linien, die viele Pixel mit einer hohen Gradientengröße durchlaufen. Wenn wir die 180 Linien in jedem Pixel mit hoher Gradientengröße betrachten, können wir nach den Linien suchen, die in mehreren dieser Pixel erscheinen, und definitiv behaupten, dass dies die Kanten im Bild sind.
Es ist jedoch fast unmöglich, exakt denselben (r, Θ) zu finden in zwei getrennten Pixeln, da wir für r nicht auf ganze Zahlen beschränkt sind. Daher müssen wir die Zeilen finden, die am ehesten sind Pixel mit hoher Gradientengröße durchlaufen.
Das Farbeimerproblem und das eigentliche Problem, das wir lösen müssen, sind eigentlich ziemlich ähnlich. Beim Farbeimerproblem haben wir nach einer ungefähren Farbe gesucht, die in Bezug auf Farbton und Wert am häufigsten vorkommt. Hier müssen wir eine ungefähre Linie finden, die unter allen Linien am häufigsten vorkommt, die durch Pixel mit hoher Gradientengröße in Bezug auf r und Θ verlaufen.
Wir können hier tatsächlich die gleiche Lösung anwenden, die wir für das Farbeimerproblem verwendet haben! Wir erstellen ein Zahlenraster von Θ =0° bis Θ =179°, wenn Sie sich vertikal bewegen, und von r =-d bis r =d, wenn Sie sich horizontal bewegen, wobei d die Hypotenuse der Bildabmessungen ist. Für jedes Pixel im Bild finden wir jede Linie, die durch dieses Pixel verläuft, und addieren den Wert der Gradientengröße zu jeder Position im Gitter, die einer der Linien entspricht.
Dieser Vorgang wird als Voting in der Hough-Transformation bezeichnet, weil wir für jede Linie "Stimmen" für die Position im Raster berechnen, die ihr selbst am ähnlichsten ist, und die Positionen mit den meisten Stimmen die Kanten sind, nach denen wir suchen.
Am Ende müssen die Orte mit den höchsten Nummern eine (r, Θ) haben Linie, die durch viele Punkte mit hoher Gradientengröße verläuft. Daher sind diese Stellen eigentlich die Ränder des Bildes in Hesse-Normalform.
Am Ende dieses Prozesses können wir die Kanten des Bildes nachzeichnen. Wir haben tatsächlich einige vielversprechende Ergebnisse!

Wie Sie oben sehen können, haben wir die Ränder des Dokuments in Rot erkannt. Da es sich um Linien und nicht um Segmente handelt, haben wir nicht an den Ecken des Dokuments angehalten, aber wir können leicht die Schnittpunkte dieser Linien finden, um die Ecken des Dokuments zu finden, was einer der letzten Schritte für unseren Dokumentenscanner ist !
Abschluss
Es gibt zwei Optimierungen, die wir an diesem Algorithmus vornehmen können. Lassen Sie uns rekapitulieren. Nachdem wir die Gradientengröße des Bildes gefunden haben, iterieren wir durch jedes Pixel und finden Linien für jeden Winkel von 0° bis 179°, die in Form von (r, Θ) durch dieses Pixel gehen (Hessische Normalform). Für jede dieser 180 Zeilen verwenden wir den Wert von Θ unverändert und runden den Wert von r auf eine ganze Zahl, um eine Zeile und Spalte in einem Zahlenraster zu berechnen. Wir addieren dann die Gradientengröße am ursprünglichen Pixel zum Eintrag im Gitter. Am Ende entsprechen die Positionen im Raster mit den größten Werten Zeilen in (r, Θ) das sind höchstwahrscheinlich Kanten.
Im Moment nehmen wir an, dass jeder Winkel von 0° bis 179° gleich wahrscheinlich ist, dass eine Gerade durch einen beliebigen Punkt geht. Wenn Sie sich jedoch an den vorherigen Artikel erinnern, haben wir tatsächlich die Gradientengröße UND die Gradientenrichtung vom Sobel-Operator. Wir wissen, dass die Gradientenrichtung die Richtung des steilsten Anstiegs für die Intensität des Bildes ist, also sollte sie eigentlich bei jedem Pixel fast senkrecht zur Kante sein.
Um sich diese Tatsache vorzustellen, stellen Sie sich vor, Sie stehen am Rand einer Klippe, und stellen Sie sich Ihre Entfernung vom Erdmittelpunkt als Funktion Ihrer seitlichen Position vor. Sie würden dem Erdmittelpunkt viel näher kommen, wenn Sie nach vorne gehen würden, während eine Bewegung in eine andere Richtung Ihre vertikale Position nicht so stark verändern würde, sodass die Richtung des Gradienten nach vorne gerichtet ist. (Ich empfehle nicht, dies experimentell zu überprüfen.)
Wenn Sie einen Schritt zurückgingen, würden Sie sich vom Rand der Klippe entfernen. Die Richtung der eigentlichen Kante der Klippe verläuft zu Ihrer Linken und Rechten, also senkrecht zur Richtung des Gefälles.
Mit dem Wissen, dass Kanten nahezu senkrecht zum Gradienten verlaufen, können wir aufhören anzunehmen, dass jeder Winkel gleich wahrscheinlich ist. Für jeden Punkt im Bild erlauben wir nur den Linien, die bei jedem Pixel fast senkrecht zum Farbverlauf stehen, statt jeden Winkel zu prüfen.
Die andere Optimierung besteht darin, die Größe jedes Behälters im Raster anzupassen. Ich fand empirisch heraus, dass ein Winkelunterschied von einem Grad tatsächlich ein ziemlich wesentlicher visueller Unterschied war. Ich habe mich entschieden, stattdessen eine Ganzzahl von 0 bis 255 zu verwenden, um den Winkel darzustellen, nicht nur, weil dadurch die Größe jedes Kästchens 0,7° statt 1° beträgt, sondern auch, weil Werte von 0 bis 255 in ein einzelnes Byte passen, was nett war aus praktischen Gründen behandeln.
Der Gitterteil der Hough-Transformation nahm jedoch bereits viel Speicherplatz in Anspruch, und mit dieser Änderung war die Menge mehr, als ich zufrieden war. Daher habe ich die Größe der Bins für r von 1 auf 2 erhöht. Dadurch wurde die benötigte Speichermenge halbiert, aber nur der maximale Fehler für die erkannten Kanten von einem Pixel auf zwei Pixel erhöht, was fast nicht wahrnehmbar ist.
Schlussfolgerungen
Kurz gesagt, wir haben mathematische Darstellungen der Kanten im Bild gefunden, indem wir die Hough-Transformation auf die Ausgabe des Sobel-Operators angewendet haben. Das ist möglich, weil jedes kantenähnliche Pixel für alle Zeilen stimmt, auf denen es liegen könnte, und wir nehmen die Zeilen mit den meisten Stimmen am Ende als die tatsächlichen Kanten im Bild.
Am Ende dieses Prozesses haben wir im Grunde eine Menge (r, Θ) gefunden Zeilen, die möglicherweise könnten stellen die Kanten des Dokuments dar, das wir zu finden versuchen ... oder sie könnten einfach die Kanten eines Schreibtischs, Ordners oder Tabletts sein, die sich zufällig im Hintergrund des Bildes befinden. Erinnern Sie sich an das Bild, das ich Ihnen zuvor gezeigt habe, wobei nur die Ränder des Dokuments erkannt wurden? Das war nach VIEL Verschönerung. Hier ist die tatsächliche Ausgabe.

Wir haben immer noch die Ränder des Dokuments, aber es gibt eine Menge Duplikate aufgrund von Unvollkommenheiten in unseren Algorithmen, von denen die meisten nur Schätzungen waren. Wir haben auch ein paar Fehlalarme:Der Stift, das kleine Notizbuch und die Tastatur im Hintergrund sahen für unseren Algorithmus alle wie Kanten aus.
Wir brauchen eine Möglichkeit, die Fehlalarme und Duplikate herauszufiltern und dabei die tatsächlichen Ränder des Dokuments beizubehalten. Dann müssen wir die vier Kanten finden, die am wahrscheinlichsten unser Dokument sind, und ihre Ecken verwenden, um den Dokumenterkennungscode fertigzustellen. Im nächsten Artikel werden wir also die Non-Max-Unterdrückung besprechen und wie ich eine heuristische vierseitige Bewertungsfunktion entworfen habe.
