logo

Erstellen eines mobilen Dokumentenscanners ohne Abhängigkeiten:Der Sobel-Operator

Wenn Sie den vorherigen Artikel in dieser Reihe (Divide and Conquer) verpasst haben, sollten Sie ihn zuerst lesen, damit Sie verstehen, was wir hier besprechen werden.

Der Sobel-Operator nähert die Gradientengröße und -richtung eines Bildes an einem bestimmten Pixel an, kann aber theoretisch auf jede diskrete Funktion zweier Variablen angewendet werden. Für diejenigen, die sich nicht erinnern oder sich nicht mit der Kalkül mit mehreren Variablen befasst haben, lassen Sie uns diskutieren, was das bedeutet. Andernfalls können Sie, wenn Sie mit Analysis vertraut sind, die nächsten Abschnitte dieses Artikels überspringen.

Derivate

Mathematische Funktionen mit einer einzelnen Variablen verwenden eine einzelne numerische Eingabevariable und erzeugen eine einzelne numerische Ausgabe. Einfach, oder? Hier ist ein Beispiel:

f ( x ) = 3 x s p ein c e f ( 0 ) = 0 f ( 2 ) = 6 f ( 10101 ) = 30303 f(x) =3x\newline\vphantom{space}\newlinef(0) =0\newlinef(2) =6\newlinef(10101) =30303 f(x)=3xspacef(0)=0f(2)=6f(10101)=30303

Wenn wir das in JavaScript schreiben würden:

function f(x) {
  return 3 * x;
}
console.log(f(1)) // 3
console.log(f(2)) // 6
// You get the idea...

Wenn wir die Ausgabe auf einer vertikalen Achse und die Eingabe auf der horizontalen Achse darstellen (d. h. y = f(x) ), erhalten wir diese nette Zeile:

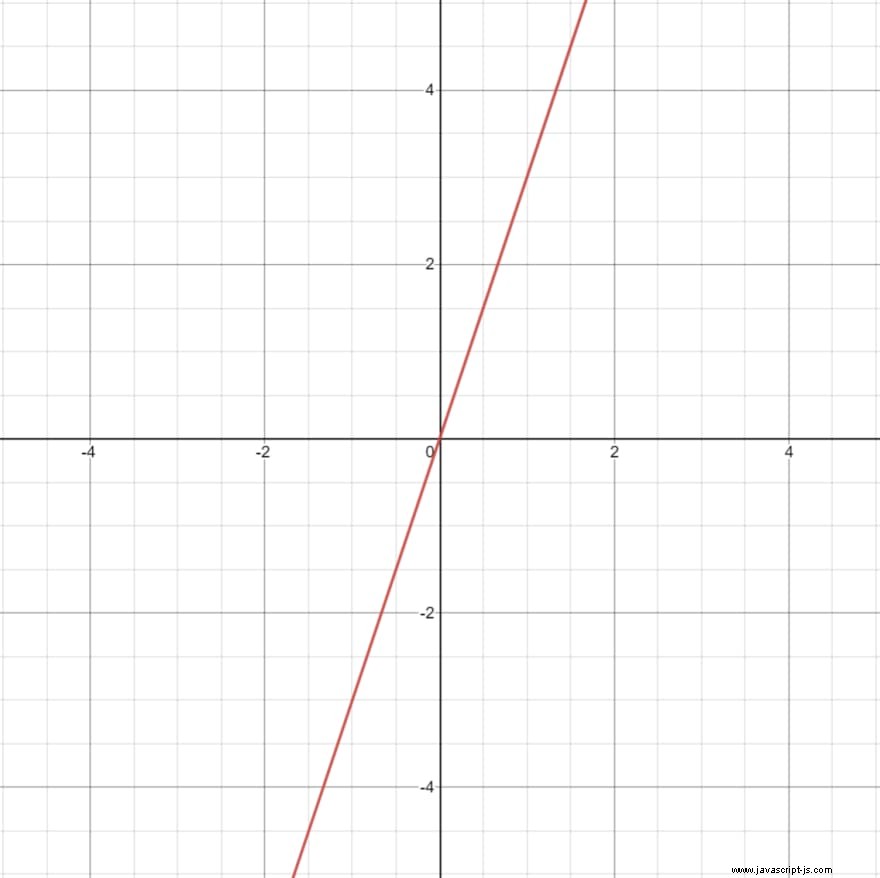
Das wissen Sie natürlich bereits. Die Dinge werden etwas interessanter, wenn wir die Steigung dieser Linie berechnen, die eine numerische Darstellung der "Steilheit" der Linie ist und durch Berechnung von "Rise Over Run" berechnet wird. Steilere Funktionen haben größere Steigungen. In diesem Fall steigt die Funktion jedes Mal um 3, wenn sie um 1 läuft (der y-Wert steigt jedes Mal um 3, wenn x um 1 steigt). Daher beträgt die Steigung 3 / 1 , oder 3. Wir hätten auch sehen können, dass es jedes Mal um 6 ansteigt, wenn es um 1 läuft, und wir würden die Steigung als 6 / 2 finden , was ebenfalls 3 ergibt.

Genauer gesagt stellt die Steigung die Änderungsrate einer Funktion dar, oder wie stark sich die Ausgabe der Funktion bei einer Änderung der Eingabe von 1 ändert.

Was ist die Steigung einer komplizierteren Funktion, sagen wir

g ( x ) = x 2 g(x) =x^2 g(x)=x2

? Wenn wir es zeichnen, sehen wir, dass die Funktion steiler wird, je weiter Sie von x = 0 gehen , also kann die Steigung nicht einfach durch eine einzelne Zahl dargestellt werden.

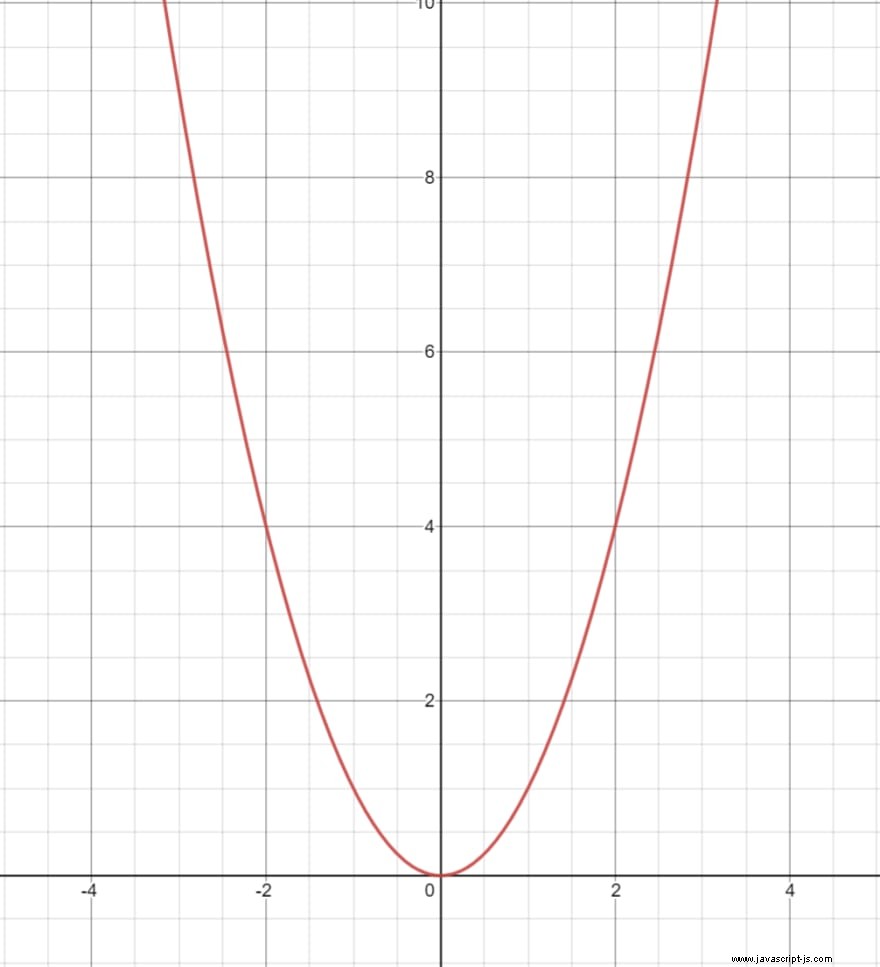
Wie sich herausstellt, hat diese Funktion nicht wirklich eine Steigung. Wir können nur die Steigungen der Tangenten für jeden Wert von x berechnen. Die Tangente ist eine lineare Annäherung an die ursprüngliche Funktion, die in der Nähe eines Punktes damit identisch ist. Hier ist ein Diagramm der Funktion mit einer Tangente bei x = 1 :

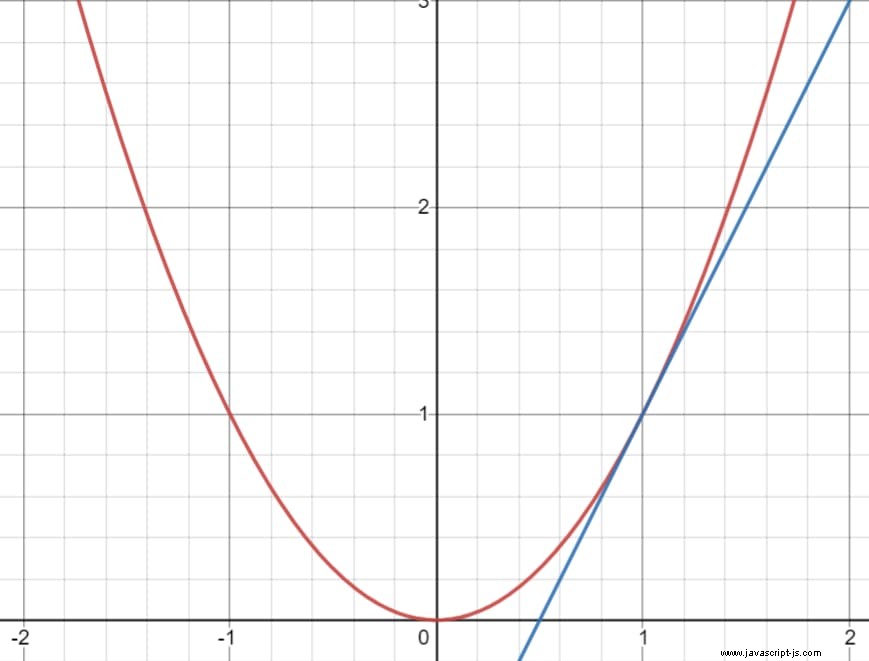
Die blaue Linie scheint mit der roten Kurve in der Nähe von x = 1 identisch zu werden , seit (1, 1) ist der Tangentialpunkt. Wie ich oben erwähnt habe, können wir die Steigung der Tangente an jedem Punkt der roten Kurve berechnen. Für diese Funktion stellt sich heraus, dass die Steigung der Tangente gleich 2x ist an jeder x-Koordinate. Wir nennen dies die Ableitung der Funktion; die Ableitung wird oft mit einem Apostroph bezeichnet, das wir „prime“ nennen. Deshalb:

f ( x ) = 3 x f ′ ( x ) = d f d x = 3 s p ein c e g ( x ) = x 2 g ′ ( x ) = d g d x = 2 x f(x) =3x\newlinef'(x) =\frac{\mathrm{d} f}{\mathrm{d} x} =3\newline\vphantom{space}\newlineg(x) =x^2\ newlineg'(x) =\frac{\mathrm{d} g}{\mathrm{d} x} =2x f(x)=3xf′(x)=dxdf​=3spaceg(x)=x2g’(x)=dxdg​=2x

Wir können sagen, dass „f-Primzahl von x 3 ist und g-Primzahl von x 2x ist“, weil für f(x) , die Tangente ist eigentlich die gleiche wie die Funktion selbst (eine Eigenschaft aller linearen Funktionen) und daher ist die Ableitung nur die Steigung, während für g(x) Wir müssen noch etwas arbeiten, um die Steigung der Tangente zu finden. Warum uns die Ableitung so wichtig ist, erfahren Sie gleich.

Die Ableitung einer Funktion ist die momentane Änderungsrate dieser Funktion. Ich möchte diesen Artikel nicht nur über Mathematik schreiben, deshalb habe ich viele Details übersprungen, die Sie wirklich lernen sollten, wenn Sie sich noch nie mit Analysis beschäftigt haben (einschließlich der Frage, wie Sie tatsächlich die Ableitung für eine beliebige Funktion berechnen!). Empfehlenswert ist der Calculus 1-Kurs der Khan Academy oder dieses hervorragende Video, wenn Sie es eilig haben.

Multivariable Funktionen

Multivariable Funktionen sind für Mathematikstudenten oft verwirrend, aber als Programmierer benutzt man sie ständig! Sie sind nur Funktionen, die mehr als eine Eingabevariable haben. Hier ist ein Beispiel:

f ( x , y ) = 3 x + y 2 f(x, y) =3x + y^2 f(x,y)=3x+y2

In JavaScript ist das nur:

function f(x, y) {
  return 3 * x + y * y;
}

Es ist ein bisschen schwieriger, sich das mental vorzustellen, da wir dies nicht mehr auf einer 2-D-Ebene grafisch darstellen können; Wir bräuchten eine 3-D-Oberfläche, um zu zeigen, wie das aussieht. Die Funktion hat sowohl eine x-Achse als auch eine y-Achse für die Eingabe und verwendet jetzt eine z-Achse für die Ausgabe. In der folgenden Abbildung ist die z-Achse vertikal und die x- und y-Achse horizontal.

Es macht keinen Sinn, diese Funktion abzuleiten:Es ist eine 3D-Oberfläche, keine Kurve, also gibt es unendlich viele Tangentenlinien, die Sie an jedem Punkt nehmen können (x, y, f(x, y)) in alle Richtungen.

Wir können es jedoch nehmen Sie die Ableitung, wenn wir angeben, in welche Richtung unsere Tangente auf der horizontalen Ebene zeigt. Beispielsweise können wir die Steigung der Tangente in positiver x-Richtung berechnen. Dies nennt man die partielle Ableitung nach x. Wir können dies für jede beliebige Richtung tun, aber in vielen Fällen kümmern wir uns nur um die Teiltöne in Bezug auf die Eingabevariablen (in diesem Fall x und y). Für diese Funktion:

f ( x , y ) = 3 x + y 2 s p ein c e ∂ f ∂ x = 3 s p ein c e ∂ f ∂ y = 2 y f(x, y) =3x + y^2\newline\vphantom{space}\newline\frac{\partial f}{\partial x} =3\newline\vphantom{space}\newline\frac{\partial f }{\partial y} =2y f(x,y)=3x+y2space∂x∂f​=3space∂y∂f​=2y

Das bedeutet, dass die partielle Ableitung nach x 3 ist , und der Teil in Bezug auf y ist 2y . Partielle Ableitungen zu bilden ist sehr einfach, wenn Sie wissen, wie man Ableitungen berechnet:Betrachten Sie alle anderen Variablen als Konstanten, wenn Sie nach einer differenzieren. Wenn wir zum Beispiel den Teil in Bezug auf x nehmen, nehmen wir einfach an, dass y ein konstanter Wert ist und können daher y^2 ignorieren Begriff. (Sie können jedoch nicht einfach davon ausgehen, dass die Werte Null sind; der Teil in Bezug auf x von xy ist immer noch y.)

Es gibt einen nützlichen Wert für stetige Funktionen mit mehreren Variablen, der als Gradientenvektor bezeichnet wird. Wenn Sie mit Vektoren vertraut sind, ist der Gradient für eine Funktion aus zwei Variablen (x und y) wie folgt definiert:

∇ f = ⟨ ∂ f ∂ x , ∂ f ∂ y ⟩ \nabla f =\left\langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right\rangle ∇f=⟨∂x∂f​,∂y∂f​⟩

In vielen Fällen interessieren wir uns wirklich nur für die Gradientenrichtung und -größe (die den Vektor ohnehin eindeutig definieren). Für jedes spezifische x und y ist die Gradientenrichtung die Richtung des „steilsten Anstiegs“, d. h. die Richtung in der XY-Ebene, in der die Ausgabe der Funktion am stärksten zunimmt, während die Gradientengröße der Wert der Ableitung in ist Gradientenrichtung (mit anderen Worten, die Steigung der steilsten Tangentenlinie in eine beliebige Richtung bei (x, y, f(x, y))). ). So berechnen Sie diese Werte (die Balken stellen die Größe dar und Theta ist der Winkel):

∣ ∇ f ∣ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 s p ein c e θ = ein t a n 2 ( ∂ f ∂ y , ∂ f ∂ x ) | \nabla f | =\sqrt{\left(\frac{\partial f}{\partial x}\right)^2 + \left(\frac{\partial f}{\partial y}\right)^2}\newline\vphantom {space}\newline\theta =\mathrm{atan2}\left(\frac{\partial f}{\partial y}, \frac{\partial f}{\partial x}\right) ∣∇f∣=(∂x∂f​)2+(∂y∂f​)2​spaceθ=atan2(∂y∂f​,∂x∂f​)

Wenn Sie noch nie mit multivariablen Kalkülen gearbeitet haben, mag das alles verwirrend erscheinen, aber es sollte sich mit der Zeit ziemlich intuitiv anfühlen, wenn Sie die vorläufige Kalküle wirklich verstehen! Auch hier ist die Khan Academy Ihr Freund.

Wo ist die Computer Vision?

Sie fragen sich vielleicht, wie sich all diese theoretischen Berechnungen tatsächlich auf das Scannen von Dokumenten anwenden lassen. Zuerst müssen Sie Ihre Vorstellung davon, was ein Bild ist, überdenken.

Sie wissen wahrscheinlich bereits, dass Bilder lediglich massive Pixelgitter sind, wobei jedes Pixel einen Rot-, Grün- und Blau- und möglicherweise einen Alpha-Wert (Opazität) hat. Jeder dieser Werte reicht typischerweise von 0 bis 255 (d. h. ein Byte repräsentiert jede Farbe/jeden Kanal). Indem Sie die Werte jedes Kanals variieren, können Sie praktisch jede Farbe aus einem einzelnen Pixel erstellen, und zusammen ergeben diese Farben ein Bild, das auf dem Bildschirm angezeigt werden kann.

Vereinfachen wir die Dinge ein wenig, indem wir stattdessen ein Graustufenbild betrachten. Jetzt gibt es nur noch einen Kanal pro Pixel, der die Intensität darstellt. Hören wir auch auf, Kanäle in Form von Bytes zu betrachten und stattdessen nur als reelle Zahlen (ein Fließkommawert statt einer ganzen Zahl). Wir haben also ein Raster aus reellen Zahlen, die die Helligkeit des Bildes an jedem Pixel oder effektiv an jedem Punkt im Raster darstellen. Versuchen Sie sich nun vorzustellen, dass dieses Bild eigentlich nur eine Funktion von x und y (die die Koordinaten jedes Pixels darstellen) ist, die eine Ausgabe der Bildintensität hat. Wenn zum Beispiel das Pixel in der dreißigsten Spalte von links und der achten Zeile von unten eine Helligkeit von 0,5 hat, könnten wir Folgendes sagen:

f ( 30 , 8 ) = 0,5 f(30, 8) =0,5 f(30,8)=0,5

Eine Frage, die Ihnen vielleicht durch den Kopf geht, lautet:„Wie genau kann ein Bild eine Funktion sein? Wir haben keine Intensität zwischen Pixelwerten. Was ist f(30.27, 8.13)? ?"

Obwohl die meisten Funktionen, denen Sie in normalen Mathematikkursen begegnen werden, einen Definitionsbereich aller reellen Zahlen haben (d. h. sie sind an jedem möglichen endlichen Punkt definiert), sind einige Funktionen nicht überall definiert. Beispiel:f(x) = 1 / x ist nicht auf Null definiert, weil 1 / 0 ist nicht vorhanden. Das Bild wird nur an den spezifischen ganzzahligen Koordinaten definiert, wo das Bild ein Pixel hat, aber es qualifiziert sich immer noch als eine Funktion. Also kurz f(30.27, 8.13) existiert nicht, f(12, 1.5) auch nicht oder f(-1, 100) .

Nehmen wir nun an, wir wollen den Gradienten dieses Bildes finden. Genau wie alle anderen Funktionen von mehr als einer Variablen sollte es möglich sein, den Gradienten zu nehmen, oder? Leider haben wir ein Problem:Es ist unmöglich, die Ableitung einer Funktion an einem Punkt zu nehmen, an dem sie nicht stetig ist, daher können wir die partiellen Ableitungen nicht berechnen und den Gradienten nicht finden.

Daher ist das Beste, was wir tun können, eine Annäherung des Gradienten des Bildes zu berechnen. Im Laufe der Jahre wurden mehrere heuristische und theoretische Methoden zum Schätzen des Gradienten entdeckt, aber eine der frühesten Techniken, der Sobel-Operator, ist nach wie vor beliebt, da sie relativ kostengünstig ist und gleichzeitig für die meisten Anwendungen genau genug bleibt.

Der Sobel-Operator spezifiziert zwei Faltungskerne, die verwendet werden können, um die partiellen Ableitungen in Bezug auf x und y bei jedem Pixel zu berechnen. Beliebte Varianten der Sobel-Kerne sind wie folgt:

S x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] s p ein c e S y = [ 3 10 3 0 0 0 − 3 − 10 − 3 ] S_x =\begin{bmatrix}-3 &0 &3 \newline-10 &0 &10 \newline-3 &0 &3\end{bmatrix}\newline\vphantom{space}\newlineS_y =\begin{bmatrix}3 &10 &3 \newline0 &0 &0 \newline-3 &-10 &-3\end{bmatrix} Sx​=⎣⎡​−3−10−3​000​3103​⎦⎤​LeerzeichenSy​=⎣⎡​30−3​100−10​30−3​⎦⎤​

Für jede der obigen Matrizen findet die Faltung jeden 3x3-Pixel-Bereich im Bild und multipliziert jede Intensität mit dem entsprechenden Wert in der Matrix und summiert dann die Ergebnisse. Die berechneten partiellen Ableitungen gelten für das zentrale Pixel (das die zweite Reihe, zweite Spalte in jeder Matrix wäre). Unter Verwendung der partiellen Ableitungen ist es trivial, die Gradientengröße und -richtung zu berechnen.

Hier ist ein tolles Video, das Faltungen mit einigen netten Visualisierungen viel detaillierter erklärt. Sie werden sogar lernen, wie einige neuronale Netze funktionieren!

Dieser Algorithmus hat sich nach jahrelanger Forschung und Tests als effektiv erwiesen, sodass Sie nicht verstehen müssen, warum er bei der Annäherung des Gradienten so gut funktioniert. Sie sollten jedoch in der Lage sein, eine allgemeine Vorstellung davon zu bekommen, was es tut.

Betrachten Sie das Sx Matrix. Wenn die Intensitäten links und rechts des mittleren Pixels etwa gleich sind, können wir davon ausgehen, dass sich in x-Richtung um das mittlere Pixel nicht viel ändert. Somit heben sich die gewichteten Werte gegenseitig auf, da der Filter über die zweite Spalte symmetrisch ist und die berechnete partielle Ableitung 0 ist. Im folgenden Beispiel sind die Pixelwerte jedoch sehr unterschiedlich:

[ 0,72 0.42 0.14 0,81 0,08 0,32 0,56 0,63 0,44 ] \begin{bmatrix}0.72 &0.42 &0.14 \newline0.81 &0.08 &0.32 \newline0.56 &0.63 &0.44\end{bmatrix} ⎣⎡​0.720.810.56​0.420.080.63​0.140.320.44​⎦⎤​

Da sich die Werte stark ändern, muss die Änderungsrate logischerweise hoch sein, also muss auch die partielle Ableitung in Bezug auf x groß sein. Es wird geschätzt auf:

− 3 ∗ 0,72 + 0 ∗ 0,42 + 3 ∗ 0,14 + − 10 ∗ 0,81 + 0 ∗ 0,08 + 10 ∗ 0,32 + − 3 ∗ 0,56 + 0 ∗ 0,63 + 3 ∗ 0,44 = − 7,00 -3 * 0,72 + 0 * 0,42 + 3 * 0,14 + \newline-10 * 0,81 + 0 * 0,08 + 10 * 0,32 + \newline-3 * 0,56 + 0 * 0,63 + 3 * 0,44 \newline=-7,00 −3*0,72+0*0,42+3*0,14+−10*0,81+0*0,08+10*0,32+−3*0,56+0*0,63+3*0,44=−7,00

Da die maximal mögliche Größe der Ableitung bei dieser Faltung 16 beträgt, ist eine Größe von 7 relativ hoch.

Es ist sehr wichtig zu beachten, dass die vom Sobel-Operator berechneten Gradienten nur im Verhältnis zueinander sinnvoll sind, da eine Änderung der Gewichtungen die maximale Größe der berechneten Ableitung ändern würde. Wenn Sie die partielle Ableitung für eine tatsächliche mathematische Funktion und nicht für ein Bild berechnen möchten, würde der Sobel-Operator nicht nur ungenaue Ergebnisse liefern, sondern auch falsch skaliert werden. Eine geeignetere Technik zum Schätzen der partiellen Ableitung in Bezug auf x auf Proben einer tatsächlichen, mathematisch ausdrückbaren Funktion wäre die Anwendung des folgenden Faltungskerns:

S x = [ 0 0 0 − 0,5 0 0,5 0 0 0 ] S_x =\begin{bmatrix}0 &0 &0 \newline-0.5 &0 &0.5 \newline0 &0 &0\end{bmatrix} Sx​=⎣⎡​0−0,50​000​00,50​⎦⎤​

Dieser Filter findet die Steigung einer linearen Annäherung der Funktion unter Verwendung der zwei Punkte, die eine Einheit vom Mittelpunkt in x entfernt sind, was eine theoretisch genauere Schätzung der Ableitung ist.

Zusammenfassend:Mit einigen mathematischen Techniken können Sie den Gradientenvektor für jeden Punkt in einem Bild schätzen, obwohl diskrete Funktionen wie Bilder eigentlich keine Ableitungen haben.

Warum ist uns der Farbverlauf eines Bildes wichtig?

Kommen wir zurück zu dem, was der Farbverlauf tatsächlich darstellt. Es beschreibt die größte Änderungsrate, die Sie an irgendeinem Punkt in einer Funktion in irgendeiner Richtung finden können. Für unser Bild codiert der Gradient die größte Intensitätsänderung, die um ein bestimmtes Pixel herum existiert. Wenn Sie darüber nachdenken, sind das, was wir visuell als "Ränder" von Dingen betrachten, die wir in einem Bild sehen, eigentlich nur Pixelpositionen, an denen sich die Intensität dramatisch ändert.

Beispielsweise ändert sich am Rand eines Blattes Papier die Intensität von fast 1 (weiß) innerhalb des Papiers auf die Intensität des Hintergrunds über drei Pixel hinweg, was zu einer hohen Gradientengröße an Kantenpixeln führt, während innerhalb des Papiers jeder 3x3-Bereich wird an allen Stellen Werte nahe eins haben, was eine sehr niedrige Gradientengröße ergibt. Wenn wir also die Gradientengröße eines Bildes nehmen, betonen wir effektiv die Kanten aller Objekte im Bild, während wir Bereiche mit geringer Änderung (d. h. das Innere dieser Objekte) unterdrücken. Ein anschauliches Beispiel soll dies verdeutlichen. Originalbild:

Gradientengröße:

Beachten Sie, dass die Ränder des Papiers fast weiß sind und der Umriss des Textes auf der Seite grau ist, während der Rest des Bildes fast schwarz ist. Dies ist der kritischste Schritt der Kantenerkennung und daher eine der Schlüsselkomponenten dieser App zum Scannen von Dokumenten.

Es ist wichtig zu beachten, dass wir vor der eigentlichen Sobel-Kantenerkennung normalerweise eine Gaußsche Unschärfe verwenden, um die Auswirkungen von Bildrauschen zu reduzieren (die aufgrund der zufälligen Intensitätsspitzen, die sie verursachen, oft als Kanten erkannt werden). Darüber hinaus haben wir das Bild erheblich verkleinert, bevor wir diesen Vorgang überhaupt gestartet haben, um die Verarbeitungszeit zu verkürzen.

Zu diesen Schritten kommen wir jedoch in zukünftigen Artikeln gegen Ende dieser Serie. Als Nächstes besprechen wir, wie wir dieses Gradientengrößenbild verwenden können, um mithilfe der Hough-Transformation tatsächlich mathematische Darstellungen der Kanten im Bild zu finden.