Poté, co operátor Sobel poskytne gradient obrázku, jsme většinou na cestě k nalezení okrajů dokumentu. Pokud nevíte, co je Sobelův operátor, důrazně doporučuji přečíst si nejprve předchozí článek ze série.
Vizuální znázornění hran však není užitečné; potřebujeme mít matematické reprezentace pro každou hranu v obrázku, abychom našli jejich průsečíky (rohy dokumentu), pro které můžeme použít Houghovu transformaci.
Houghova transformace nám umožňuje najít nedokonalé shody pro libovolné vizuální vzory pomocí bucketovaného systému hlasování. Existují dva způsoby, jak porozumět tomuto algoritmu:matematický a intuitivní. Pojďme si projít obojí, než probereme, jak to můžeme implementovat.
Matematicky
Protože Houghova transformace může technicky najít kruhy, elipsy, trojúhelníky nebo jakýkoli jiný libovolný vzor, potřebovali bychom individuální matematickou analýzu pro každý typ vzoru, který chceme detekovat.
Pro účely tohoto projektu jsme hledali čáry, pro které byla původně navržena Houghova transformace, a jsou proto nejsnáze detekovatelným typem vzoru. (Pokud vás zajímá, proč nehledáme jen obdélníky, abychom našli dokument, dostaneme se k tomu na konci.
Nejprve se rozhodneme, jak chceme naše čáry matematicky znázornit. Přirozenou volbou může být slavný:
y=mx+b
Tato forma nám umožňuje reprezentovat jakoukoli přímku, která by mohla existovat ve 2D prostoru, úpravou parametrů m (sklon přímky) ab (průsečík y). Pokud chceme čáru se sklonem 30 stupňů, která je 1200 pixelů od spodní části obrázku, můžeme použít:
m=tan30°b=1200spacey=0,577x+1200To vypadá vizuálně přesně i při vykreslování:
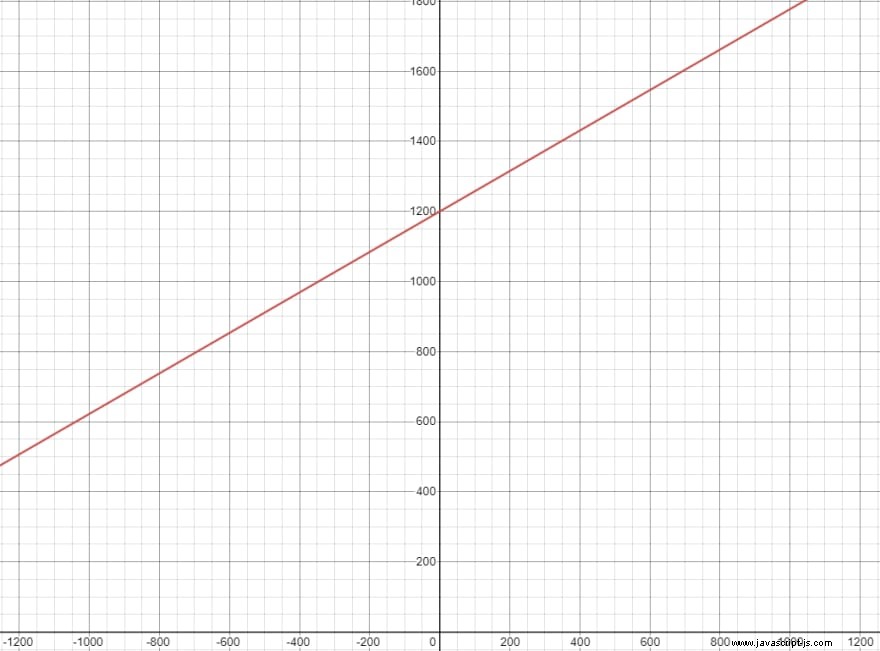
Jediným problémem této reprezentace je to, co se stane, když se pokusíme vytvořit svislou čáru. Vertikální čáry se nepohybují vodorovně, jejich průběh je vždy nula a jejich stoupání je libovolné číslo. Technicky můžeme k vyjádření sklonu použít kladné nebo záporné nekonečno, ale pak bychom neměli žádný způsob, jak zjistit, kde na ose x se přímka nachází, protože tato rovnice specifikuje pouze průsečík y.
Ačkoli je možné tento problém obejít, je také důležité vzít v úvahu skutečnost, že chceme být schopni rozlišovat mezi vizuálně odlišnými liniemi, ale tato forma to ztěžuje. Zvažte tyto čtyři řádky:
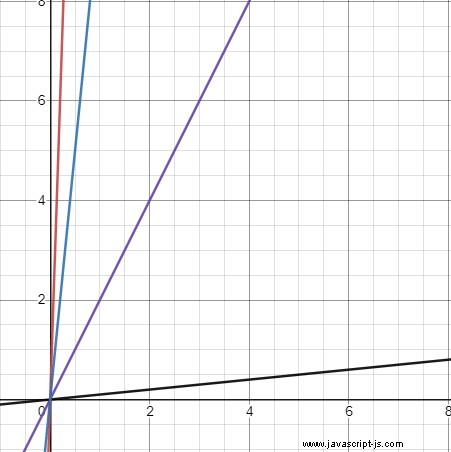
Černá čára má sklon 0,1 (tj. m =0,1), fialová čára 2, modrá čára 10 a červená čára 30.
Přestože vizuálně jsou červené a modré čáry vizuálně velmi podobné, jejich sklony se liší o 20, a přestože se fialové a černé čáry zdají odlišné, jejich sklony se liší pouze o 1,9. Pokud chceme použít sklon, museli bychom najít nějaký způsob, jak zdůraznit malé rozdíly ve sklonu při nižších hodnotách.
Místo abychom se zabývali všemi těmito problémy, můžeme čáry znázornit přesněji pomocí polárních souřadnic.
"Normální" souřadnice jsou také známé jako kartézské souřadnice:jsou reprezentovány jako (x, y) , kde x je umístění na vodorovné ose ay je umístění na svislé ose. Polární souřadnice jsou místo toho reprezentovány jako (r, Θ) , kde r je vzdálenost od počátku a theta je úhel proti směru hodinových ručiček od toho, co by byla kladná osa x v kartézských souřadnicích. Zde je několik příkladů:
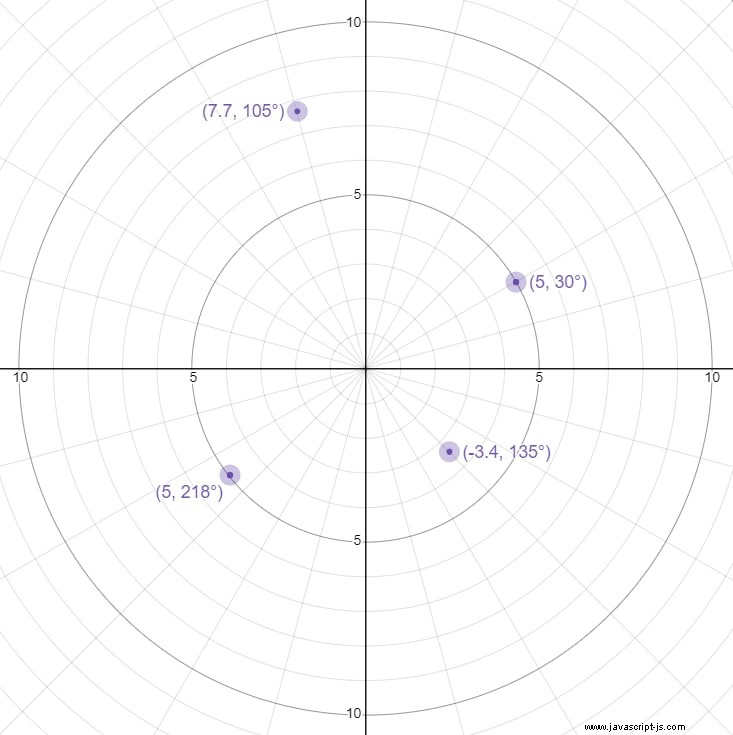
Polární souřadnice a kartézské souřadnice vždy splňují následující rovnice:
x=rcosθy=rsinθspacer=x2+y2θ=atan2(y,x)
I když můžeme převést náš původní tvar y = mx + b do polární, skončili bychom se stejnými problémy kolem vizuální podobnosti a svislých čar. Místo toho můžeme použít Hesseovu normální formu, která může reprezentovat čáry pomocí jediné polární souřadnice.
Většina online vysvětlení dělá Hesse normální formu složitější, než je pro naše účely nutné, takže zde je intuitivní vysvětlení. Představte si, že máte libovolnou polární souřadnici. Nakreslete segment od počátku k této souřadnici. Nyní nakreslete čáru kolmou k segmentu, který obsahuje souřadnici. Tato čára je jednoznačně identifikována polární souřadnicí.
Zde je graf, jak to vypadá:
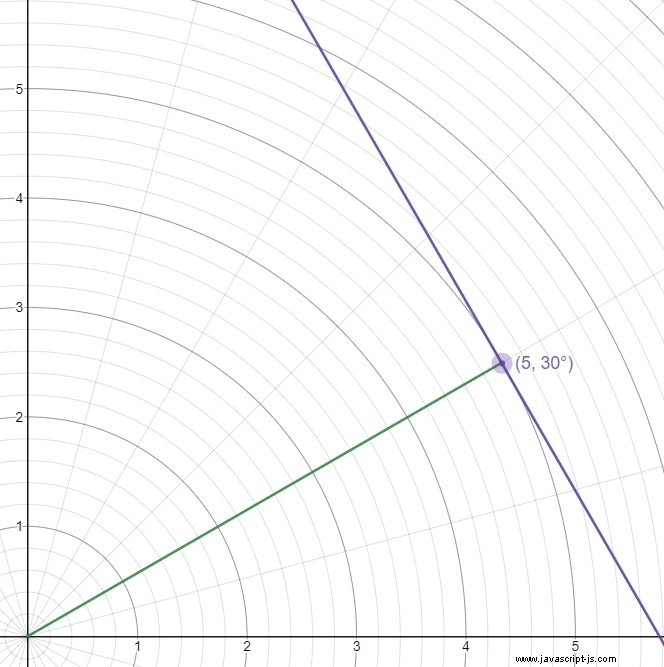
Zelená úsečka spojuje počátek s bodem, takže kolmá fialová čára je čára, kterou můžeme popsat pomocí bodu (5, 30°) .
To nám dává snadný způsob, jak rozlišit čáry:pokud jsou body daleko od sebe, čáry se vizuálně liší. Již neexistují případy, kdy malá změna v proměnné způsobí velkou vizuální změnu čáry, protože r a theta mají každý "lineární" vizuální efekt. Například změna theta o 10° vždy způsobí podobný vizuální rozdíl pro čáru, bez ohledu na to, jaká je přesná hodnota theta.
Ještě důležitější je, že Hesseova normální forma usnadňuje nalezení čar, na kterých leží jakákoliv souřadnice v kartézském prostoru. Pokud známe úhel Θ v hessenské normální formě a máme kartézskou souřadnici (x, y) tato čára prochází, můžeme vyřešit pro r:
Ve výše uvedené rovnici jakékoli dva body, které leží na stejné úsečce úhlu Θ, vytvoří stejnou hodnotu r. Brzy si probereme, proč je tato kvalita tak důležitá. Prozatím poskytnu intuitivní vysvětlení procesu hlasování v Houghově transformaci.
Kbelíky barvy
Představte si, že máte za úkol najít nejběžnější barvu barvy z jednoho milionu kbelíků.
Jedním z řešení by mohlo být projít každý kbelík a poznamenat si, kolik kbelíků jste viděli u každé barvy. Tento přístup však nabízí velmi omezenou přesnost:nemůžete zadat přesnou barvu, ale spíše něco obecného jako „zelená“ nebo „žlutá“. Toto řešení navíc nebere v úvahu odchylky v množství barvy na kbelík.
Lepším řešením by bylo vytvořit velkou mřížku prázdných nádrží s barvou, kde posunutím mřížky nahoru získáte jasnější barvy a posunutím na kteroukoli stranu získáte jiný odstín. Jinými slovy, mohli bychom najít, kde v následujícím grafu leží jednotlivé barvy:
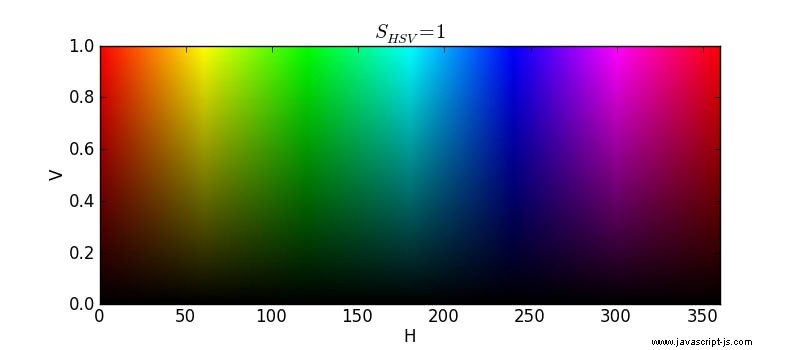
Vím, že tento graf nebere ohled na sytost, ale pro účely tohoto příkladu můžeme předpokládat, že každá barva barvy je plně sytá.
Představte si, že ve výše uvedeném grafu jsou mřížky podél každého stupně odstínu a každé zvýšení hodnoty o 0,01. Můžeme odhadnout odstín a hodnotu každého kbelíku barvy a poté vysypat obsah kbelíku do nádrže v mřížce odpovídající tomuto odstínu a hodnotě.
Pokud například narazíme na kbelík s tmavě červenou barvou, vylijeme ji do jedné z nádrží v levém dolním rohu mřížky (protože spodní oblast má tmavší barvy a levá oblast červené).
Nakonec jsme mohli najít nádrže s nejvíce barvou, abychom určili nejběžnější barvu v laku.
Tento přístup řeší dva problémy s naším původním přístupem sčítání. Vzhledem k tomu, že vyléváme kbelíky do mřížky, přesně zohledňujeme všechny rozdíly v množství barvy na kbelík. Ještě důležitější je, že naším konečným výsledkem je přesná barva a teoreticky je maximální chyba oproti skutečné nejběžnější barvě plocha jedné nádrže (chyba jednoho stupně v odstínu a chyba 0,01 v hodnotě).
Je důležité poznamenat, že tento přístup by byl špatnou volbou, pokud bychom neměli tolik kbelíků barvy jako datových bodů. Pokud by například existovalo jen několik tisíc kbelíků, většina z 18 000 nádrží by byla po vylití veškeré barvy zcela prázdná a drobné chyby v naší aproximaci barvy by způsobily nesprávné výsledky.
Pokud bychom například našli deset kbelíků s téměř přesně stejným odstínem žluté s mírně odlišným jasem, mohli bychom je umístit do deseti samostatných nádrží, zatímco dvě jasně červené kbelíky, u kterých jsme odhadli, že mají přesně stejný odstín a jas, by se vešly dovnitř. stejná nádrž. Nakonec bychom v jasně červené nádrži našli dvě kbelíky barvy a v každé žluté nádrži jen jeden kbelík, takže náš algoritmus rozhodl, že červená je nejběžnější barva, i když žlutá byla jasně převládající.
Kam tato analogie směřuje?
Pokud si vzpomínáte z dříve, diskutovali jsme o tom, jak nám Hesseova normální forma umožňuje reprezentovat jakoukoli čáru s bodem v polárních souřadnicích a jak lze vizuálně podobné čáry znázornit souřadnicemi, které jsou matematicky blízko sebe. Pojďme diskutovat o tom, jak jej můžeme skutečně použít k nalezení čar v našem obrázku s přechodem.
Pro každý pixel v obrázku můžeme najít všechny čáry procházející obrázkem, na kterých by pixel mohl ležet. Prozatím budeme předpokládat, že čára v každém směru je možná. Můžeme zacyklit od Θ =0° do Θ =179° v krocích po jednom stupni a vyřešit pro r pomocí rovnice z dříve, abychom našli 180 potenciálních čar v hessenském normálním tvaru (r, Θ) na pixel. (Všimněte si, že nejdeme na 359°, protože čáry se rozprostírají nekonečně ve dvou opačných směrech, takže jakýkoli úhel nad 180° poskytuje čáru identickou s některým úhlem pod 180°.)
Nyní tedy máme v obrázku 180 matematických řádků na pixel. Co s tím vlastně můžeme dělat?
Pamatujte, že se snažíme najít čáry, které odpovídají hranám v obrázku; jinými slovy čáry, které procházejí mnoha pixely s velkým gradientem. Pokud vezmeme v úvahu 180 řádků v každém pixelu s vysokou velikostí gradientu, můžeme hledat řádky, které se objevují ve více těchto pixelech, a rozhodně tvrdit, že se jedná o okraje v obrázku.
Je však téměř nemožné najít přesně stejný (r, Θ) ve dvou samostatných pixelech, protože nejsme omezeni na celá čísla pro r. Proto musíme najít řádky, které jsou nejvíce procházet pixely s vysokým gradientem.
Problém kbelíku s barvou a skutečný problém, který musíme vyřešit, jsou ve skutečnosti dost podobné. V problému s kbelíkem barvy jsme hledali přibližnou barvu laku, která byla nejběžnější z hlediska odstínu a hodnoty. Zde musíme najít přibližnou čáru, která je nejběžnější ze všech čar procházejících pixely s vysokou gradientovou velikostí ve smyslu r a Θ.
Můžeme vlastně použít stejné řešení, jaké jsme použili pro problém s kbelíkem barvy zde! Vytvoříme mřížku čísel v rozsahu od Θ =0° do Θ =179° při svislém pohybu a od r =-d do r =d při vodorovném pohybu, kde d je přepona rozměrů obrázku. Pro každý pixel v obrázku najdeme každou čáru, která tímto pixelem prochází, a ke každé pozici v mřížce, která odpovídá jedné z čar, přidáme hodnotu velikosti gradientu.
Tento proces je známý jako hlasování v Houghově transformaci, protože na každém řádku počítáme "hlasy" pro pozici v mřížce, která je jí nejpodobnější, a pozice s největším počtem hlasů jsou okraje, které hledáme.
Na konci musí mít místa s nejvyššími čísly (r, Θ) čára, která prochází mnoha body s velkým gradientem. Proto jsou tato místa ve skutečnosti okraji obrazu v hessenské normální formě.
Na konci tohoto procesu můžeme obkreslit okraje obrázku. Máme skutečně slibné výsledky!

Jak můžete vidět výše, okraje dokumentu jsme detekovali červeně. Protože se jedná o čáry a ne o segmenty, nezastavili jsme se u rohů dokumentu, ale můžeme snadno najít průsečíky těchto čar, abychom našli rohy dokumentu, což je jeden z posledních kroků pro náš skener dokumentů. !
Dokončení
U tohoto algoritmu můžeme provést dvě optimalizace. Pojďme si to zrekapitulovat. Po zjištění velikosti gradientu obrázku iterujeme každý pixel a najdeme čáry každého úhlu od 0° do 179°, které procházejí daným pixelem ve smyslu (r, Θ) (Hessenská normální forma). Pro každý z těchto 180 řádků použijeme hodnotu Θ tak, jak je, a zaokrouhlíme hodnotu r na celé číslo, abychom vypočítali řádek a sloupec v mřížce čísel. Poté přidáme velikost gradientu v původním pixelu k záznamu v mřížce. Pozice v mřížce s nejvyššími hodnotami nakonec odpovídají řádkům v (r, Θ) to jsou s největší pravděpodobností okraje.
V tuto chvíli předpokládáme, že každý úhel od 0° do 179° je stejně pravděpodobný pro přímku procházející jakýmkoli daným bodem. Pokud si však pamatujete z předchozího článku, ve skutečnosti máme velikost gradientu A směr gradientu od Sobelova operátoru. Víme, že směr přechodu je směr nejstrmějšího vzestupu intenzity obrazu, takže by měl být v každém pixelu téměř kolmý k okraji.
Abyste si tuto skutečnost představili, představte si, že stojíte na okraji útesu, a přemýšlejte o své vzdálenosti od středu Země jako funkci vaší boční polohy. Pokud byste udělali krok vpřed, přiblížili byste se mnohem blíže středu Země, zatímco pohyb jakýmkoli jiným směrem by vaši vertikální polohu tolik nezměnil, takže směr gradientu je vpřed. (Nedoporučuji to experimentálně ověřovat.)
Kdybyste ustoupili dozadu, vzdálili byste se od okraje útesu. Směr skutečné hrany útesu je nalevo a napravo, tj. kolmo ke směru sklonu.
S využitím znalosti, že hrany jsou téměř kolmé na gradient, můžeme přestat předpokládat, že každý úhel je stejně pravděpodobný. Pro každý bod na obrázku povolíme hlasovat pouze čáry téměř kolmé na gradient v každém pixelu namísto kontroly každého úhlu.
Další optimalizací je úprava velikosti každého zásobníku v mřížce. Empiricky jsem zjistil, že jeden stupeň rozdílu v úhlu byl ve skutečnosti docela podstatný vizuální rozdíl. Rozhodl jsem se místo toho použít k vyjádření úhlu celé číslo od 0 do 255, nejen proto, že velikost každého pole byla 0,7° místo 1°, ale také proto, že hodnoty od 0 do 255 se vešly do jednoho bajtu, což bylo příjemné. řešit z praktických důvodů.
Mřížková část Houghovy transformace však již zabírala hodně paměti a s touto změnou bylo množství více, než jsem byl spokojen. Proto jsem zvětšil velikost přihrádek pro r z 1 na 2. Tím se množství potřebné paměti snížilo na polovinu, ale pouze se zvýšila maximální chyba detekovaných hran z jednoho pixelu na dva pixely, což je téměř nepostřehnutelné.
Závěry
Stručně řečeno, našli jsme matematické reprezentace hran v obrázku použitím Houghovy transformace na výstup Sobelova operátoru. To je možné, protože každý pixel podobný hraně hlasuje pro všechny řádky, na kterých by mohl ležet, a řádky s největším počtem hlasů na konci považujeme za skutečné okraje v obrázku.
Na konci tohoto procesu jsme v podstatě našli spoustu (r, Θ) čáry, které by mohly potenciálně představují okraje dokumentu, který se snažíme najít... nebo to mohou být jen okraje stolu, složky nebo tabletu, které byly náhodou na pozadí obrázku. Pamatujete si ten obrázek, který jsem vám ukázal dříve, přičemž byly detekovány pouze okraje dokumentu? To bylo po VELKÉM zkrášlování. Zde je skutečný výstup.

Stále máme okraje dokumentu, ale existuje spousta duplikátů kvůli nedokonalostem v našich algoritmech, z nichž většina byly pouze odhady. Máme také několik falešných poplachů:pero, malý notebook a klávesnice na pozadí vypadaly jako hrany našeho algoritmu.
Potřebujeme způsob, jak odfiltrovat falešně pozitivní a duplikáty a přitom zachovat skutečné okraje dokumentu. Potom musíme najít čtyři okraje, které budou pravděpodobně naším dokumentem, a použít jejich rohy k dokončení kódu detekce dokumentu. Takže v příštím článku probereme non-max potlačení a jak jsem navrhl heuristickou čtyřúhelníkovou skórovací funkci.
